
We can determine this limit by seeing what f(x) equals as we get really large values of x. But you can use limits to see what the function ought be be if you could do that. Since ∞ is not a number, you cannot plug it in and solve the problem. The other thing limits are good for is finding values where it is impossible to actually calculate the real function's value - very often involving what happens when x is ±∞. So, this function has a discontinuity at x=3.īut lim x→3 f(x) = 6, because, it looks like the function ought to be 6 when you get close to x=3, even though the actual function is different. If the function is not continuous, even if it is defined, at a particular point, then the limit will not necessarily be the same value as the actual function.
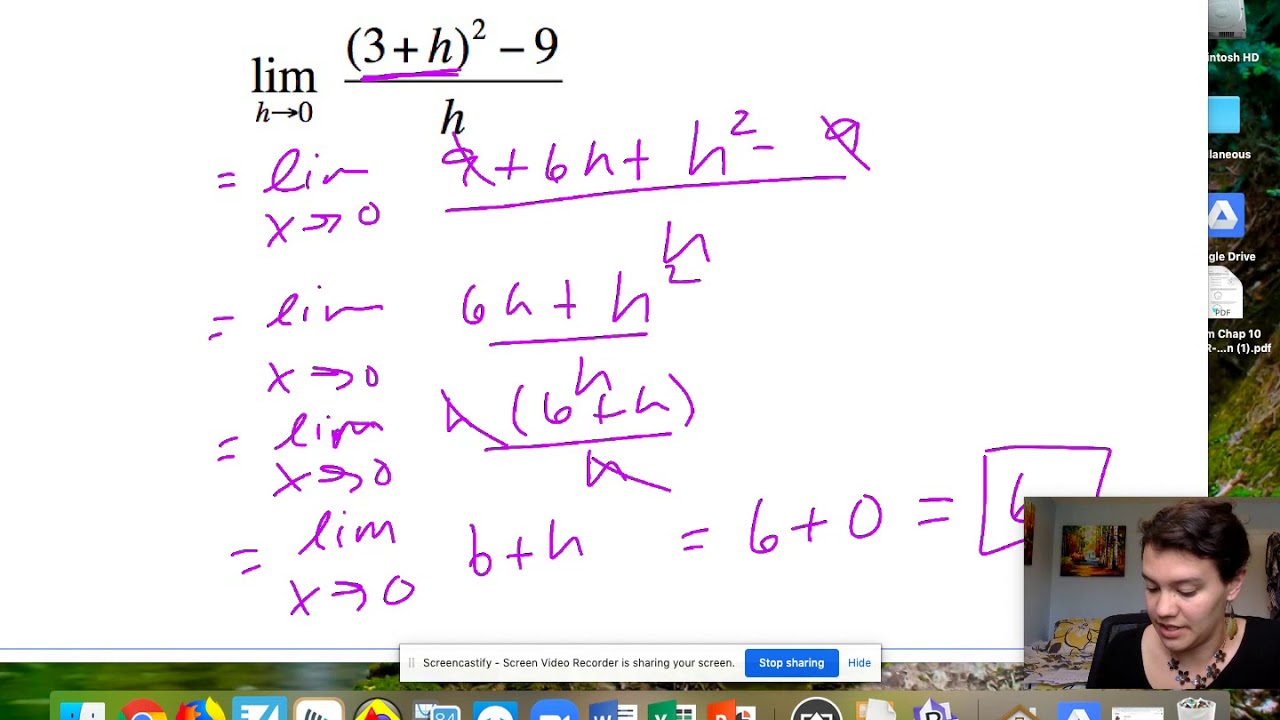
In fact, that is one way of defining a continuous function:į(c) = lim x→c⁻ f(x) = lim x→c⁺ f(x) for all values of c within the domain.īut, suppose that there is something unusual that happens with the function at a particular point. If you have a continuous function, then this limit will be the same thing as the actual value of the function at that point. Many aspects of calculus also have geometric interpretations in terms of areas, slopes, tangent lines, etc.Ī limit is a method of determining what it looks like the function "ought to be" at a particular point based on what the function is doing as you get close to that point. The reason you see a lot of, say, algebra in calculus, is because many of the definitions in the subject are based on the algebraic structure of the real line. Some calculus courses focus most on the computational aspects, some more on the theoretical aspects, and others tend to focus on both. Elementary calculus is also largely concerned with such questions as how does one compute the derivative of a differentiable function? How does one compute the integral of an integrable function? Here there are many techniques to be mastered, e.g., the product rule, the chain rule, integration by parts, change of variable in an integral. One should regard these theorems as descriptions of the various classes.Īnd then there is, of course, the computational aspect. If one knows that a function ƒ is continuous, what else can you say about ƒ? The intermediate value theorem, the extreme value theorem, and so on, are examples of theorems describing further properties enjoyed by continuous functions.

For instance, an integrable function may be less smooth (in some appropriate sense) than a continuous function, which may be less smooth than a differentiable function, which may be less smooth than a twice differentiable function, and so on. Some insight will reveal that this process of grouping functions into classes is an attempt to categorize functions with respect to how "smooth" or "well-behaved" they are. Examples of such classes are the continuous functions, the differentiable functions, the integrable functions, etc. One divides these functions into different classes depending on their properties. I don’t have to say it again do I? (the whole thing about we are looking near x not at x… there I said it…)Īs you continue to study limits, the plan is to develop ways to find limits without using the graph, but being able to find a limit this way can give you a much better understanding of exactly what a limit is, even if you aren’t using the formal definition.Elementary calculus may be described as a study of real-valued functions on the real line. Remember: I don’t care what is happening when \(x=1\), I only care about what is happening what \(x\) is close to 1!įrom the picture above, I can see that \(\lim_ f(x)\) does not exist, even though \(f(-1)=-4\). We are going to find two limits: The limit of \(f(x)\) as \(x\) approaches 1 from the right and the limit as \(x\) approaches 1 from the left. Now for an actual example! I have graphed the function \(f(x)=x^2+1\) below. If we are interested in what is happening to the function \(f(x)\) as \(x\) gets close to some value \(c\) from the left, we write:
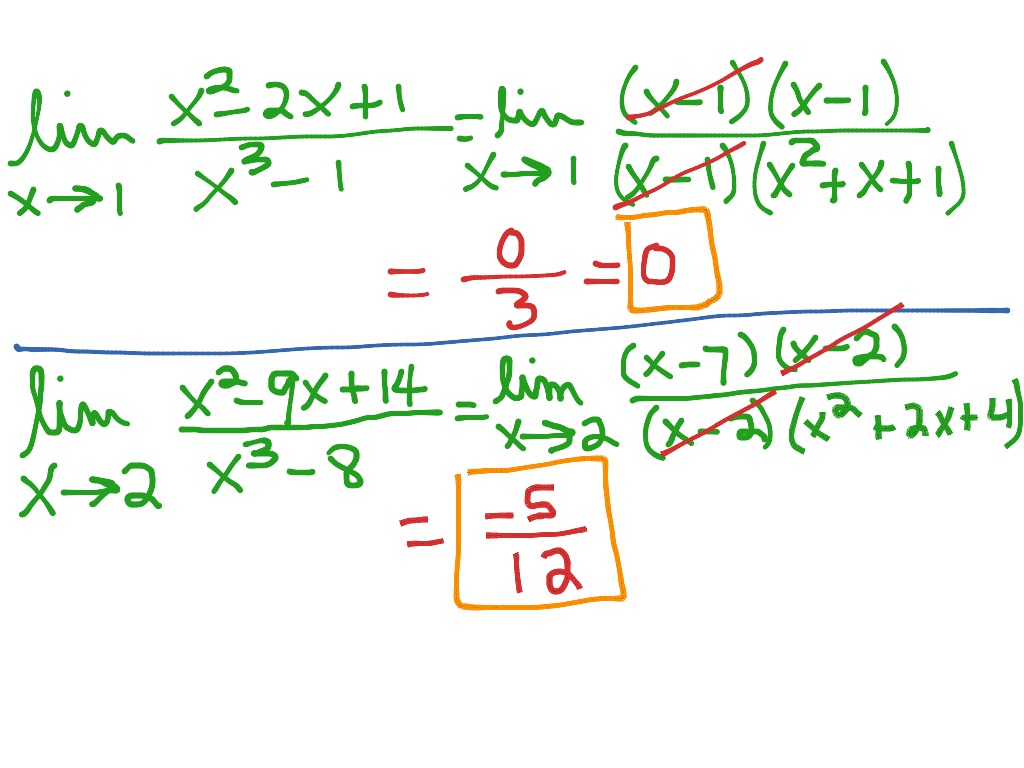
If we are interested in what is happening to the function \(f(x)\) as \(x\) gets close to some value \(c\) from the right, we write: When I talk about the limit of a function \(f(x)\) as \(x\) approaches some value, I am not saying “what is \(f(x)\) at this value” like I might in algebra! Instead, I am interested in what is happening to \(f(x)\) when \(x\) is close to this value. Calculus involves a major shift in perspective and one of the first shifts happens as you start learning limits.


 0 kommentar(er)
0 kommentar(er)
